Hur Man Beräknar Roulette-Sannolikheter (Matematiskt)

“The very name ‘calculus of probabilities’ is a paradox. Probability opposed to certainty is
what we do not know, and how can we calculate what we do not know?”
Henry Poincaré

Trots allt prat om sannolikheter och statistik verkar det som om få människor faktiskt kan beräkna matematiskt chansen för ett givet rouletteutfall. Ibland använder de sig av Excel eller specialprogram för att testa miljontals snurr för att komma med rätt nummer. När någon förstår grundläggande sannolikhet kan man svara på nästan alla frågor angående säkerheten för alla resultat med bara en enkel räknare eller bara sätta ekvationen som en formel i en enkel excel-fil (online baccarat).

Först måste vi förstå vad som är den faktiska funktionen, som har symbolen:!
Det betyder att multiplicera en serie med fallande naturliga tal.
Exempel:

4! = 4 × 3 × 2 × 1 = 24
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
1! = 1
0!=1 (axiomatiskt)

Praktiskt taget för rouletteändamål, visar en faktor hur många olika sätt, olika objekt (eller nummer) kan ordnas. Utan repetitioner av samma objekt eller nummer. För att ge dig en uppfattning om hur stort detta antal kan bli, för 37 nummer, som i europeisk spela roulette:
37! = 1,3763753 × 1043
Det innebär att det finns många biljoner biljoner olika arrangemang av de 37 online roulette numren. Utan att räkna med de möjliga upprepningarna av siffror. Bara på hur många olika sätt (sekvenser) kan alla roulette nummer visas på 37 spins. Du kan läsa mer om matematiska kombinationer här.

SANNOLIKHETSEKVATIONEN

Här är den huvudsakliga matematiska formeln för att beräkna chansen för ett rouletteutfall eller händelse.
Först måste vi definiera parametrarna:

P (e) är sannolikheten för en händelse E.
n är antalet försök (snurr)
x är antalet gånger vår insats vinner
P (b) är sannolikheten för att vår satsning B vinner i ett snurr

Sannolikheten P (e) för händelsen E = [Bet b visas x gånger i n snurr] =

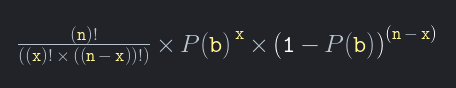
en gång till:

P(e) = (n!/(x!(n-x)!)) P(b)x (1-P(b))n-x

Om du vill förstå denna ekvation ännu djupare kan du undersöka Binomial distribution som är grunden för de flesta casino live roulette-sannolikheter. Jag vill också betona den viktiga skillnaden mellan sannolikhet och förväntan. Här är en snabb och enkel metod för att beräkna risken i Spela gratis roulette och den här artikeln hjälper dig att förstå och beräkna det förväntade värdet på varje insats.

Låt oss nu se hur kraftfull den här metoden är i handling. Följande exempel hjälper dig att bättre förstå hur formeln fungerar.

ENKLA CHANCER EXEMPEL

Låt oss säga att vi vill beräkna sannolikheten för två svarta i tre snurr. Eller för att uttrycka det annorlunda ”hur ofta kommer vi att se exakt två svarta nummer i tre snurr”. Observera att denna ekvation beräknar de exakta sannolikheterna för en specifik händelse. Inte sannolikheten för 2 eller fler svarta, men exakt 2 svarta.
Parametrarna är:

n = 3 (totalt snurr)
x = 2 (svarta siffror / vinnande snurr)
P (b) = 0,5 (sannolikheten för svart i varje snurr - vi ignorerar nollan för enkelhetens skull)

P(e) = (n!/(x!(n-x)!)) P(b)x (1-P(b))n-x
P(e) = (3!/(2!(3-2)!)) 0.52 (1-0.5)3-2
P(e) = (3!/(2!1!)) 0.52 0.51
P(e) = (3×2×1/2×1×1) 0.25× 0.5
P(e) = (3/1) 0.25× 0.5
P(e) = 3 × 0.125 = 0,375

Därför är sannolikheten att 3 snurr ska ha exakt 2 svarta siffror 0,375 eller 37,5% eller lite mer än 1/3. Alla dessa siffror är bara olika uttryck för samma sak - förväntan om att det ska ske ens.

DUSSINTAL EXEMPEL

Vi vill beräkna sannolikheten för att ett specifikt (inte vilket som) dussintal träffar exakt 2 gånger på 6 snurr.
n = 6
x = 2
P(b) = 12/37

P(e) = (6!/(2!(6-2)!)) (12/37)2 (1-12/37)6-2
P(e) = (6×5×4!/(2!4!)) 0.3242 0.6764
P(e) = (30/2) 0.105× 0.209
P(e) = 15 × 0,022
P(e) = 0,329 or 32,9% eller runt 1/3

 
EXEMPEL PÅ SINGELNUMMER

Du vet att i Live Casino Roulette är sannolikheten för att ett visst antal visas i en snurr 1/37 eller 2,7%. Men vad är sannolikheten för att ett visst antal visas exakt en gång på 37 snurr?

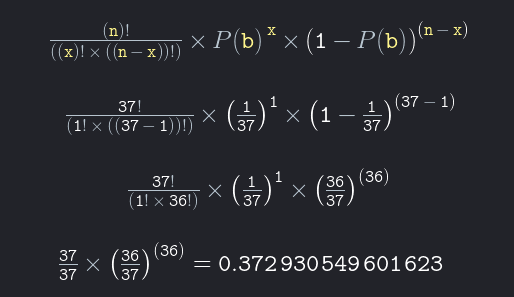
Sannolikheten för att ett visst antal visas exakt en gång under 37 snurr är 0,373 eller 37,3%.

Med samma formel kan vi beräkna sannolikheten för att ett visst antal inte visas alls på 37 snurr (0,362 eller 36,2%) och sannolikheten för att det visas två gånger (0,186 eller 18,6%).

Den matematiska formeln vi presenterade här kan användas för att hitta alla roulette-sannolikheter i form av "Bet B slår X gånger i N-snurr".

ETT NUMMER SOM UPPREPAS 3 GÅNGAR I 38 SPINS I AMERIKANSK ROULETTE

Genom att ange relevanta värden i huvudekvationen får vi:

 
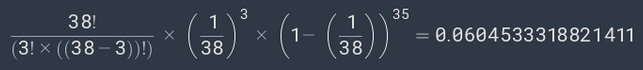
Vilket innebär att chansen att detta händer är 0,06 eller 6% eller 1 / 16,6.
Följaktligen kan vi förvänta oss att ett sådant fenomen kommer att inträffa en gång på 633 snurr. Eftersom detta på 38 snurr har sannolikhet 1/16,6, kan vi förvänta oss att det sker i genomsnitt efter 38 * 16,6 = 633 snurr.

Här är en användbar miniräknare där du kan KOPIERA och klistra in EKVATIONEN och sedan använda siffrorna.